Java 1.8 Priority Queue 代码分析

在实际生活中，队列都是有优先级的，在某些条件下不一定按照先到先得，而是按照元素的某些特性进行出队的。

• 比如游戏中 小兵的攻击并不固定，而是攻击离它最近的单位，或者是攻击血量最小的单位。
• 在医院排序看病，医生也会根据患者的患病程度进行就诊，先救治特别紧急的患者。

为什么需要优先队列？

按照优先队列的性质，每次出队取最符合“条件”的元素。

那其实也不一定需要优先队列，我用数组，或者链条其实也能实现，只不过我在添加元素的时候对元素进行排序就可以了。这样不是也能解决问题吗？

时间复杂度对比：

• 普通线性结构：入队 O(1) 出队 O(n)

• 顺序线性结构：入队 O(n) 出队 O(1)

• 堆：入队O(logn) 出队 O(logn)

优先队列可以解决什么问题？

• 在 M 个元素中，找出前 K 个元素

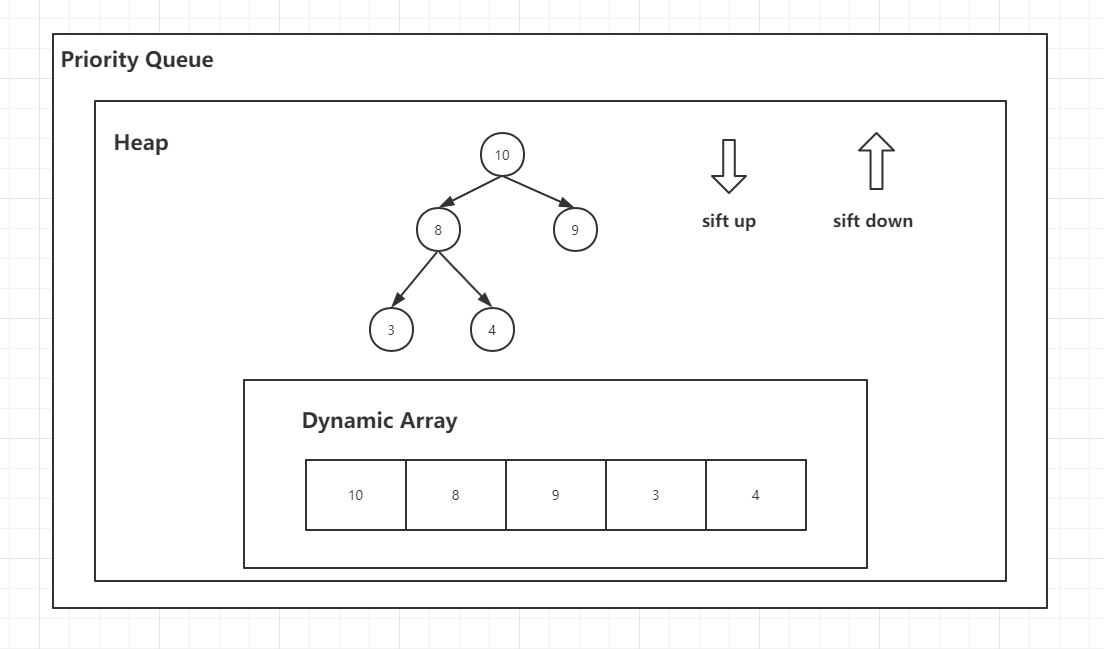
Java 1.8 的底层采用最小[堆](./数据结构 - 二叉堆.md)进行实现。

• 比较器

  PriorityQueue 构造函数中允许传入比较器用于组装堆。在初始化时便可以传入比较器。

  PriorityQueue<Integer> q = new PriorityQueue<>((o1, o2) -> o2 - o1);
  q.add(1);
  q.add(2);
  q.add(3);
  
  Integer result = q.peek();
  System.out.println(result); // 3
  

• 添加元素

  优先队列中添加元素实际上是在堆中添加元素时间复杂度为 (logn).

  // 添加指定的元素到优先队里中
  public boolean add(E e) {
      return offer(e);
  }
  
  public boolean offer(E e) {
      if (e == null)
          throw new NullPointerException();
      modCount++;
      int i = size;
      if (i >= queue.length)
          grow(i + 1);
      size = i + 1;
      if (i == 0)
          queue[0] = e;
      else
          siftUp(i, e);
      return true;
  }
  

  添加元素时，首先判断当前容器是否还能承载新元素，如果不能则进行扩容操作 grow

  如果当前堆中不还没有元素则直接添加即可，否则进行 Sift Up (上浮) 操作。

  private void siftUpComparable(int k, E x) {
      Comparable<? super E> key = (Comparable<? super E>) x;
      while (k > 0) {
          int parent = (k - 1) >>> 1;
          Object e = queue[parent];
          if (key.compareTo((E) e) >= 0)
              break;
          queue[k] = e;
          k = parent;
      }
      queue[k] = key;
  }
  

  实际就是进行上浮，与父节点进行对比，迭代交换

• 取出 “最符合条件”的元素

  添加元素的时候，其实就是已经形成了最符合条件的堆（最大堆|最小堆），根节点其实就是将要取出的节点，后续我们只需要进行 堆的下浮（Sift Down）即可。

  public E poll() {
      if (size == 0)
          return null;
      int s = --size;
      modCount++;
      E result = (E) queue[0];
      E x = (E) queue[s];
      queue[s] = null;
      if (s != 0)
          siftDown(0, x);
      return result;
  }
  

  private void siftDownComparable(int k, E x) {
      Comparable<? super E> key = (Comparable<? super E>)x;
      int half = size >>> 1;        // loop while a non-leaf
      while (k < half) {
          int child = (k << 1) + 1; // assume left child is least
          Object c = queue[child];
          int right = child + 1;
          if (right < size &&
              ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
              c = queue[child = right];
          if (key.compareTo((E) c) <= 0)
              break;
          queue[k] = c;
          k = child;
      }
      queue[k] = key;
  }